Bài viết chia sẻ khái niệm, cách tính chu vi đa giác, hỗ trợ bạn đọc hiểu và dễ dàng tìm được lời giải cho các bài toán tính chu vi, diện tích các khối hình đa giác trong chương trình học. Một vài ví dụ minh họa về cách tính chu vi đa giác cũng được cập nhật để bạn đọc ôn tập và làm quen với các dạng bài này
- Cách tính chu vi ngũ giác
- Cách tính chu vi tứ giác
- Cách tính chu vi tam giác
- Cách tính chu vi hình vuông
- Cách tính chu vi hình chữ nhật
Sau khi tìm hiểu và làm quen với các hình khối cơ bản như hình tam giác, hình vuông, hình chữ nhật, các bạn học sinh tiểu học sẽ tiếp tục được tiếp cận với các hình khối có độ khó cao hơn là hình đa giác

Tính chu vi đa giác không đều, cách tính chu vi đa giác đều.
Vậy hình đa giác là gì? Có bao nhiêu loại hình đa giác? Cách tính chu vi đa giác thế nào? Tất cả sẽ được giải đáp ở bài viết dưới đây của 9mobi.vn.
Cách tính chu vi đa giác
1. Công thức tính chu vi hình đa giác
Đa giác là một đường gấp khúc được tạo ra bởi các đoạn thẳng nối tiếp nhau và khép kín (đầu mút của điểm đầu và điểm cuối trùng nhau)
Các bạn có thể tham khảo thêm khái niệm, đặc điểm các loại đa giác trên Wiki Tại Đây
Dựa vào số lượng và kích thước của các đoạn thẳng tạo lên đa giác mà người ta phân loại đa giác thành 3 loại chính: đa giác đều, đa giác lồi và đa giác lõm
Chu vi đa giác được hiểu là độ dài đường bao quanh hình đa giác và bằng tổng chiều dài của các cạnh tạo lên đa giác.
- Công thức tính chu vi đa giác: P = a1 + a2 + a3 +... + an
Trong đó:
P là chu vi đa giác
a1, a2, a3,..., an là các cạnh của đa giác
Công thức tính chu vi đa giác được đề cập ở trên là công thức tính chu vi chung, được áp dụng cho tất cả các loại đa giác (cả đa giác đều và đa giác không đều)
Ví dụ: Tính chu vi đa giác không đều
Bài tập 1: Tính chu vi hình ngũ giác ABCDF có chiều dài các cạnh lần lượt là 12, 13, 28, 6, 19
Lời giải
Dựa vào công thức tính chu vi đa giác, ta có
- Chu vi ngũ giác ABCDF là: P(ABCDF) = 12 + 13+ 28 +6+ 19 = 78 cm
2. Công thức tính chu vi đa giác đều
- Khái niệm: đa giác đều được hiểu là đa giác có tất cả các cạnh bằng nhau và các góc ở đỉnh bàng nhau. Ví dụ về các hình đa giác đều: Tam giác đều (3 cạnh), hình vuông (4 cạnh) , hình ngũ giác đều (5 cạnh) , hình lục giác đều (6 cạnh)
- Chu vi hình đa giác đều: là trường hợp đặc biệt của các hình đa giác nên công thức tính chu vi hình đa giác đều cũng dễ tính toán hơn cả.
P (đa giác đều) = a x n
Trong đó:
P là chu vi hình đa giác đều
a là chiều dài của cạnh
n là số cạnh
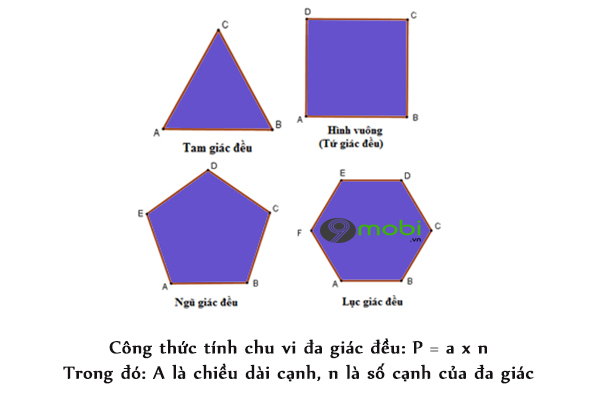
Ví dụ về các loại đa giác đều và cách tính chu vi đa giác đều
Ví dụ 2: Tính chu vi hình vuông ABCD có chiều dài 1 cạnh là 12 cm
Lời giải:
Theo công thức tính chu vi đa giác đều, ta có chu vi hình vuông ABCD là: P (ABCD) = 12 x 4 = 48cm
Ví dụ 3: Tính cạnh của lục giác đều ABCDEF khi biết chu vi bằng 108 cm
Lời giải:
Theo dữ liệu bài ra, ra có:
Theo công thức tính chu vi đa giác đều, ta có : P (ABCDEF) = 6 x AB = 108 cm
hay AB = 18 cm
Mà lục giác đều ABCDEF là hình có 6 cạnh với độ dài bằng nhau . Lúc này ta sẽ được AB = BC = CD= DE= EF= FA = 18 cm
Đáp án: Độ dài một cạnh của lục giác đều bằng 18 cm
Trên đây là một ví dụ về cách tính chu vi đa giác không đều và tính chu vi đa giác đều. Với các bài tập yêu cầu tính chu vi đa giác bằng 2 cách, các bạn có thể sử dụng công thức tính đa giác thường ở trên hoặc tìm cách chia nhỏ đa giác thành nhiều hình khối nhỏ hơn và tính chu vi (Lúc này chu vi đa giác sẽ bằng tổng chu vi của các khối nhỏ chứa trong nó).
Ở bài viết trên đây, 9mobi.vn đã chia sẻ cho bạn cách tính chu vi hình đa giác không đều, đa giác đều. Nếu như đã nắm vững khái niệm, công thứ tính chu vi của các hình tam giác, hình chữ nhật, hình vuông,..., thì việc tính chu vi đa giác cũng không thể làm khó được các bạn.
https://9mobi.vn/cach-tinh-chu-vi-da-giac-25728n.aspx
Hình thoi cũng là hình đa giác đều với 4 cạnh song song và bằng nhau. Công thức tính chu vi hình thoi cũng tương tự với cách tính chu vi hình đa giác đều. Nếu muốn tìm hiểu rõ hơn về cách tính chu vi hình thoi, các bạn có thể tham khảo bài viết này của 9mobi.vn .