Bài viết bên dưới đây 9mobi.vn sẽ hướng dẫn đến các bạn cách tính chu vi tam giác thường, tam giác đều, tam giác cân...Qua đó có thể nắm vững các công thức để giải các bài tập trong chương trình học một cách nhanh chóng, cũng như ứng dụng vào công việc hoặc trong cuộc sống hàng ngày một cách hiệu quả.
- Cách tính chu vi đa giác
- Cách tính chu vi ngũ giác
- Cách tính chu vi tứ giác
- Cách tính diện tích tam giác
- Cách tính chu vi hình vuông
Tại sao cần tính chu vi tam giác:
+ Nắm được công thức toán học trong chương trình học
+ Vận dụng vào thực tế trong công việc, cuộc sống hàng ngày để tính các vật thể tam giác thực
Tam giác là hình khối được tạo ra từ 3 điểm không thẳng hàng với và ba cạnh là các đoạn thẳng nối các điểm đó với nhau.

Khái niệm, công thức tính chu vi tam giác (tam giác thường, tam giác cân, tam giác vuông, tam giác đều)
Dựa vào tính chất các góc, các cạnh trong tam giác mà tam giác được phân chia thành 4 loại chính: tam giác thường, tam giác vuông, tam giác cân, tam giác vuông cân và tam giác đều.
Trong phạm vi bài viết này, 9mobi.vn sẽ giới thiệu cho bạn cách tính chu vi của từng dạng tam giác khác nhau, giúp các bạn tổng hợp thông tin và áp dụng để giải bài tập trên lớp, tính toán chu vi của từng loại tam giác gặp trong thực tế sau này.
Cách tính chu vi tam giác
1. Cách tính chu vi tam giác thường
Công thức tính chu vi hình tam giác thường: Chu vi tam giác bằng độ dài tổng ba cạnh của tam giác đó
P = a + b + c
Trong đó: P là chu vi tam giác, a, b, c là 3 cạnh của hình tam giác đó
Dựa theo cách tính này, chúng ta cũng có thể tìm được cách tính nửa chu vi tam giác như sau: 1/2 P = (a+b+c)/2
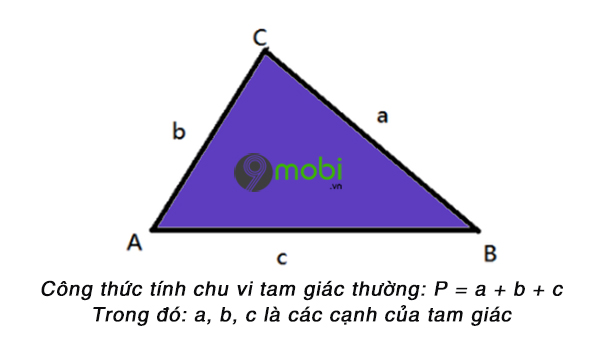
Hình ảnh tam giác thường, cách tính chu vi tam giác thường.
Ví dụ 1: Tính chu vi tam giác lớp 2
Cho tam giác với độ dài các cạnh lần lượt là 3cm , 4 cm, 5 cm. Yêu cầu tính chu vi của tam giác đó.
Lời giải: Dựa theo công thức tính chu vi tam giác, ta có: P = a + b+ c.
Theo dữ liệu bài ra thì: a = 3 cm, b = 4 cm, c = 5cm
Như vậy, chu vi của tam giác đã cho là: P = 3 + 4 + 5 = 12 cm
Ví dụ 2: Tính chu vi tam giác khi biết 3 cạnh
Cho tam giác với độ dài 2 cạnh bên lần lượt là 3, 4 cm. Biết cạnh còn lại của tam giác có độ dài gấp 2 lần tổng tam giác còn lại. Hãy tính chu vi tam giác đó.
Bài giải:
Gọi tam giác cần tính chu vi là ABC
Theo bài ra ta có: AB = 3cm, AC = 4 cm và BC = 2 (AB + AC)
Như vậy, chiều dài cạnh còn lại của tam giác là: BC = 2 (AB + AC) = 14 cm
Chu vi tam giác ABC lúc này sẽ bằng: P (ABC) = AB + AC + BC = 3 + 4 + 14 = 19 cm
2. Cách tính chu vi tam giác vuông
Khái niệm: Tam giác vuông là tam giác có một góc là góc vuông
- Công thức tính chu vi tam giác vuông: P= a + b + c
Trong đó:
+ a và b : Hai cạnh của tam giác vuông
+ c là cạnh huyền của tam giác vuông.
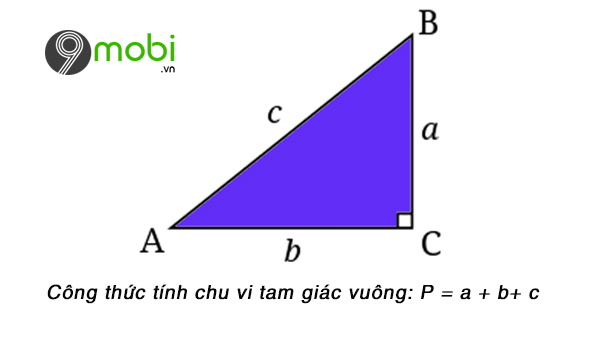
Hình ảnh tam giác vuông, cách tính chu vi tam giác vuông.
Ví dụ 3: Tính chu vi tam giác lớp 3
Cho tam giác vuông ABC với độ dài 3 cạnh lần lượt là 8 cm, 10 cm và 12 cm. Hãy tính chu vi của tam giác vuông này?
Lời giải: Dựa theo công thức tính chu vi tam giác, ta có
- Chu vi tam giác vuông ABC là: P (ABC) = 8 + 10 + 12 = 30cm
3. Cách tính chu vi tam giác cân
Khái niệm: Tam giác cân là tam giác có 2 cạnh bên bằng nhau.
- Công thức tính chu vi tam giác cân: P = 2 a + c
Trong đó a : Hai cạnh bên của tam giác cân, c là đáy của tam giác.
Công thức tính chu vi tam giác này cũng được áp dụng để tính chu vi của tam giác vuông cân (tam giác có 1 góc vuông và 2 cạnh bên bằng nhau)
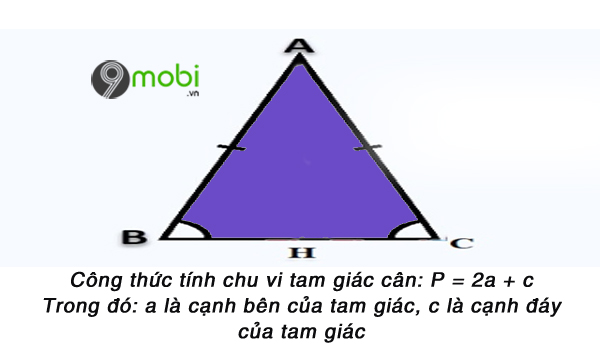
Hình ảnh tam giác cân, cách tính chu vi tam giác cân.
Ví dụ 4: Tính chu vi tam giác cân ABC khi biết chiều dài cạnh bên là 5 cm, chiều dài cạnh đáy là 8cm
Lời giải:
Vì tam giác ABC là tam giác cân nên ta có: AC = AB = 5cm
Áp dụng công thức tính chu vi hình tam giác, ta có
- Chu vi tam giác ABC là: P (ABC) = (5 x 2) + 8 = 18 cm
4. Cách tính chu vi tam giác đều
Khái niệm: Tam giác đều là tam giác có 3 cạnh bằng nhau
- Công thức tính chu vi tam giác đều: P = 3 x a
Trong đó: P là chu vi tam giác đều, a là chiều dài cạnh của tam giác
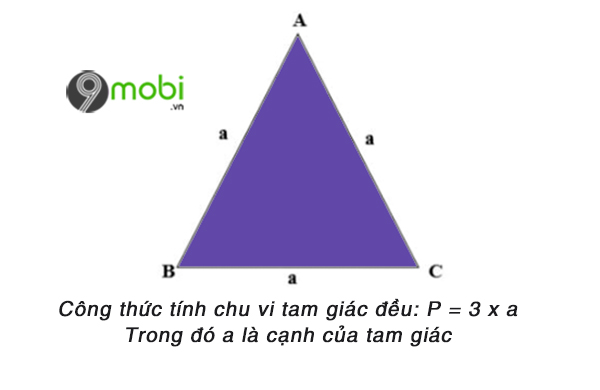
Hình ảnh tam giác đều, cách tính chu vi tam giác đều.
Ví dụ 5: Tính chu vi tam giác đều ABC với chiều dài cạnh AB = 5 cm
Lời giải:
Vì tam giác ABC là tam giác đều nên ta có, độ dài các cạnh là: AB = AC = BC = 5cm
Dựa vào công thức tính chu vi tam giác đều, ta có: P (ABC) = 5 x 3 = 15cm
Tính diện tích, chu vi hình tam giác là một trong những kiến thức cơ bản mà các em học sinh được học khi ngồi trên ghế nhà trường. Nắm được khái niệm, các loại hình tam giác và cách tính chu vi tam giác từng loại không chỉ các em dễ dàng giải các bài toán từ đơn giản đến phức tạp mà hỗ trợ rất tốt vào cuộc sống, công việc của các em sau này.
https://9mobi.vn/cach-tinh-chu-vi-tam-giac-25727n.aspx
Cùng với hình tam giác, chu vi hình chữ nhật cũng là vấn đề được nhiều người quan tâm khi học tập và làm việc. Nếu muốn tính chu vi, diện tích hình chữ nhật nhưng không nhớ công thức tính như thế nào thì bài viết giải đáp cách tính chu vi hình chữ nhật của 9mobi.vn sẽ giúp bạn gợi nhớ và tìm được câu trả lời cho bài toán của mình.